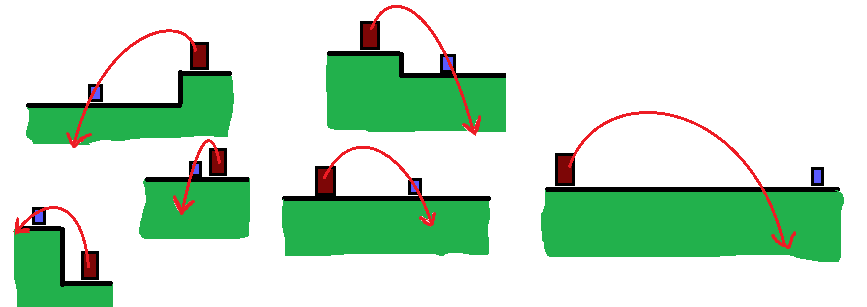
I’m trying to figure out how to calculate trajectories for throwing objects like grenades, axes, cannon balls etc.
I got this example for Unity working to some degree: http://www.aboutpixels.me/unity-2d-parabolic-trajectory-projectile-motion-calculation but it doesn’t have the curve I’d like to have. It also doesn’t have maximum velocities, which is also a problem. Doesn’t make sence that you can throw grenade from other side of the world right?
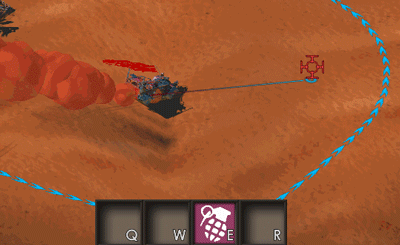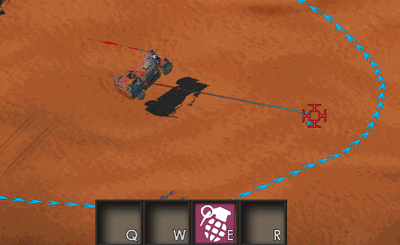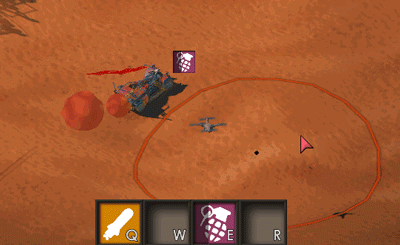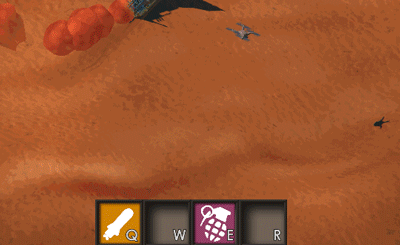
Here’s illustration how I’d want it to work:
Does anyone have example for this?
Maximum velocity should be tested BEFORE using the equation if the projectile is not self accelerated (ie not a rocket nor missile). So the initial velocity and the gravity (Ay in the example) should be enough to limit the reach.
What kind of trajectory are you expecting ?
Maybe it would be better if you did your own physics maths for this, or use a physics library
1 Like
Do you want to just throw object or calculate trajectories ? If you just want to throw them then use a physics engine like box2D or Newton.
1 Like
Just google the problem as a physics thing, don’t search for game related stuff.
It gets covered in the first semester at any science or engineering related college minor in basic physics.
The difficulty is that you have more variables that the function depends on other than the distance.
For example the maximum height of the parabola depends on the speed at which the projectile is launched AND the distance it has to cover. Alternatively if the speed is not constant, it now depends on the time it should take the projectile to reach the ground, in that case our maximum height depends on time of flight and distance.
That all assumes we always throw at the same angle, if we change angles this suddenly depends on one more thing.
For my implementation I have the time constant, but I adjust angle and speed depending on the distance to the target so that it looks more like someone who’d actually try to hit something.
Anyways, here is the implementation I made for my game. It’s pretty old and maybe not very readable, but I hope I helped you already.
Mind you that it’s 3d - x and y are the ground and z is the height component. So if you were to copy this into a 2d game your xy become xz (y is depth).
Note that the functions .Xy() return a 2 component vector with the xy of the 3 component vector.
So basically you could also write new Vector2(v3.X, v3.Y);
Vector3 difference = targetPosition- startPosition;
if (difference.Length() < 5) return;
float t = 1;
float g = -GameSettings.Gravity; // gravity
float v = difference.Xy().Length()*2f/(t*60); // velocity
float x = difference.Xy().Length()*(1.3f+FastRand.NextSingle()*0.2f); // target x + random offset (throw should not be 100% accurate)
float y = difference.Y; // target y
float s = v * v * v * v + 1*Math.Sign(y)* g * (g * (x * x) + 2 * y * (v * v)); //substitution
if (s < 0) s = v * v * v * v + g * (g * (x * x) + 2 * y * (v * v));
double o = Math.Atan((v * v + Math.Sqrt(s)) / (g * x)); // launch angle
Vector3 direction = Vector3.Normalize(new Vector3(difference.Xy(), 0));
direction.X *= (float) Math.Cos(o)*v;
direction.Y *= (float) Math.Cos(o)*v;
direction.Z = (float) (Math.Sin(o)*v);
1 Like
Thanks for the replies, but I still have the problem.
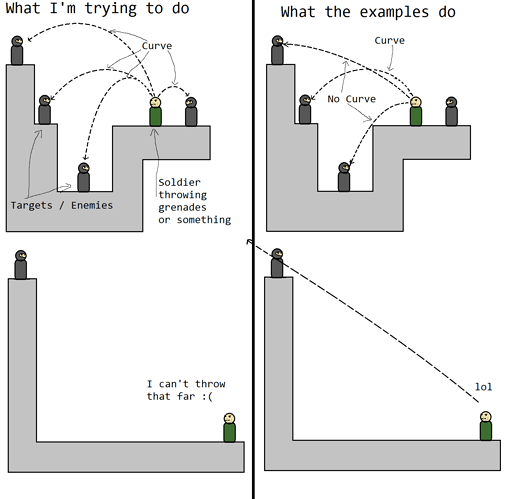
Problem isn’t to hit target; it is to have the curve and some restrictions on max velocity, sorry if it wasn’t clear in first post.
Something like Skeletons in Castlevania series, but with targeting functionality https://giphy.com/gifs/aria-castlevania-sorrow-3o7bu0av2iWJDgiiwE
Why not just build a firing angle distance table for different velocitys / guns and different heights and just approximate in between values.
One advantage is you can build and then save a tables via programmatically test firing regardless of max speed acceleration or any other variables you introduce.
That’s how they did it in the old days before computers with real life artillery.
1 Like
This is a Box2D integration I came across some time ago:
http://www.iforce2d.net/b2dtut/projected-trajectory
It comes with a nice article. Maybe you can make use of it for your own needs.
1 Like
I don’t understand what the problem is, all is in the tutorial you pointed in the first tutorial if you only want a parabolic trajectory without needing real physics precision.
1 Like
I’m bad at explaining the problem as English isn’t my native language and I’m not that good at math/physics, but here is drawing of it: