Is there something wrong with Matrix.CreateFromAxisAngle?

[John_Smith]

So I just started using MonoGame so I might be missing something obvious but it seems like the CreateFromAxisAngle function isn’t working the way it should.

I ran this code as a simple example:

Matrix curr = Matrix.CreateWorld(Vector3.Zero, Vector3.One, Vector3.Up);
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;
Debug.WriteLine($"Curr.Up:{curr.Up}\nNext.Up:{next.Up}");

And this is what it output:
Curr.Up:{X:-0.40824828 Y:0.81649655 Z:-0.40824828}
Next.Up:{X:0.17615414 Y:0.96024776 Z:0.21654965}

Clearly the two up vectors are very different but if it’s rotating around that vector then they should be the same give or take some rounding errors. This doesn’t appear to be a problem for unit vectors however.

[ed022]

I wonder if the discrepancy you’re seeing might arise from the nonorthogonal vectors in your call to CreateWorld. Looking at the source code, the “up” parameter is only used to create the “right” vector, which is then used in turn to create the resultant matrix’s “up” vector. If you provide two nonorthogonal vectors, and it tries to make an orthogonal matrix from them, you can expect some odd results.

Another possibility might be the multiplication order; what happens if you multiply them the other way around?

[John_Smith]

TBH I don’t see how any of that would affect this since I’m using the curr.Up and not Vector3.Up so assuming it successfully orthogonalized the matrix it should be the same issue. And changing the order would make it rotate in place instead of around the axis which is what I actually want, but it should also be affected by the Matrix not doing the axis rotation properly.

Testing orthogonalization:
Matrix curr = Matrix.CreateWorld(Vector3.Zero, Vector3.One, Vector3.Up + Vector3.Left);
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;
Debug.WriteLine($“Curr.Up:{curr.Up}\nNext.Up:{next.Up}”);
Results:
Curr.Up:{X:-0.7071068 Y:0.7071068 Z:0}
Next.Up:{X:0.32726988 Y:0.94326997 Z:-0.05600345}

Testing Orthonormalization:
Matrix curr = Matrix.CreateWorld(Vector3.Zero, Vector3.One * (1 / MathF.Sqrt(3)), (Vector3.Up + Vector3.Left) * (1 / MathF.Sqrt(2)));
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;
Debug.WriteLine($“Curr.Up:{curr.Up}\nNext.Up:{next.Up}”);
Results:
Curr.Up:{X:-0.70710677 Y:0.70710677 Z:0}
Next.Up:{X:0.32726997 Y:0.94326985 Z:-0.05600342}

Testing Ordering:
Matrix curr = Matrix.CreateWorld(Vector3.Zero, Vector3.One, Vector3.Up);
Matrix next = curr * Matrix.CreateFromAxisAngle(curr.Up, 1.7f);
Debug.WriteLine($“Curr.Up:{curr.Up}\nNext.Up:{next.Up}”);
Results:
Curr.Up:{X:-0.40824828 Y:0.81649655 Z:-0.40824828}
Next.Up:{X:-0.40824828 Y:0.8164965 Z:-0.40824825}

So it looks like it doesn’t have the problem when you rotate first which means than I can get the result I want by doing this:
Vector3 target = Vector3.Zero;
float distance = MathF.Sqrt(3);
Matrix curr = Matrix.CreateLookAt(Vector3.One, target, Vector3.Up);
Matrix next = curr * Matrix.CreateFromAxisAngle(curr.Up, 1.7f);
next.Translation = target + distance * next.Backward;

But if anyone knows why the initial problem exists I would still love to know…

[ed022]

Can you elaborate upon what it is you’re trying to achieve, or what your intended results are?

To ensure we’re on the same page, here’s my understanding of curr * next, as specified in your last example (as best I can illustrate - most definitely not to scale, and edited several times as I realise how poor my illustration is)

As you can see, the up vector is indeed maintained.

It looks like you’re then setting the Translation component of the matrix to what it should be as a natural result of this transformation - at least when the target is the origin. What are your observations about the need to do this? Is this where the “problem” that you’re seeing arises?

[John_Smith]

So you picture describes exactly what I want to happen which I’m pretty sure is what should happen when you run this:
Matrix curr = Matrix.CreateLookAt(Vector3.One, Vector3.Zero, Vector3.Up);
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;

The problem is that what is actually happening is very different. Easily seen by the Up vectors being different.

To test things out even more thoroughly I made a little Transform class that basically does the same functionality as Matrix and it seemed to work fine:
Transform tmp = Transform.LookAt(Point.One, Point.Zero, Point.Up);
Transform ntmp = Transform.RotateAxis(tmp.Basis.Up, 1.7f) * tmp;
Debug.WriteLine($“Curr:{tmp.Basis}\nNext:{ntmp.Basis}”);
Resulted in:
Curr:[ Right: [ X: 0.70710677, Y: 0, Z: -0.70710677 ], Up: [ X: -0.40824828, Y: 0.81649655, Z: -0.40824828 ], Front: [ X: -0.57735026, Y: -0.57735026, Z: -0.57735026 ] ]
Next:[ Right: [ X: 0.48143104, Y: 0.57253796, Z: 0.6636448 ], Up: [ X: -0.40824828, Y: 0.8164965, Z: -0.40824822 ], Front: [ X: 0.77560127, Y: 0.074388444, Z: -0.6268245 ] ]

I can provide more of the Transform code if you want to see what it’s doing internally.

[ed022]

As you pointed out in you previous reply, if you reverse the order of multiplication, the up vectors are indeed the same. Let’s make sure we understand what’s happening there, and why that reversal of Monogame’s matrices give you what you want.

You effectively have two component matrices. The one from CreateLookAt is a transformation that says “move to this position, and turn to look at this target.” The other, from CreateFromAxisAngle, says “rotate about this axis this much”. So, when you multiply them together, it compounds those two operation, and the order does matter.

If you do CreateFromAxisAngle * CreateLookAt (or CreateWorld, which both basically accomplish the same thing), which was what you did in your original post, it says “Rotate about this axis (which is going to turn the viewer onto its side), and then move and rotate that rotated viewer, as if they were upright, so as to face the target.” As you can hopefully see by this description, the raw up vector has gotten twisted around from that first transformation.

If you do it the other way around, CreateLookAt * CreateFromAxisAngle, it effectively says “Move and rotate the viewer to face the target, then rotate that about the axis at the origin.” This, it sounds like, is much closer to what you want. But as such, look at the order of the multiplication.

I’m not sure if this is where the misunderstanding is coming in, but do remember that matrices are transformations, not points. When you multiply them, you’re saying, “do this transformation, then that transformation, in this order.” The result of which is a single matrix that effectively performs both, again, in that order. It’s not saying “Transform this position as specified by my world matrix”, which could be a tempting (but misleading) way of visualising it. (Heck, even I’m kind of guilty of that in my earlier illustration.)

If I had to venture a guess, I might suspect that your Transform class is effectively transforming a transform, rather than compounding two transforms into one. That might sound like the same thing, but they’re actually kind of opposites.

[willmotil]

CreateFromAxisAngle is fine.

Your error is in the CreateWorld method you used
Vector3.One
Instead of
Vector3.Up for the forward vector.

Which will be normalized to a axis that is midway between right up forward you are then rotating about that axis by 1.7 radians some trhing like 115 degrees or so.

MonoGame/MonoGame/blob/develop/MonoGame.Framework/Matrix.cs#L1449

[John_Smith]

Why does it matter what curr is? That matrix should be fine no matter what since it orthonormalizes it.
The only reason I felt that needed to be in there is because this only works with an abnormal basis.
If you make next with:
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;
then next.Up should equal curr.Up no matter what since it’s rotating about that axis.
And I realize it’s floating point so there might be small discrepancies, but it’s flinging it all over the place.

[John_Smith]

It actually happens in the opposite order: second * first.
Everything works if you just use the 3 unit axes with CreateFromAxisAngle, it’s only when the axis starts to get weird that the issues pop up.

[ed022]

Yeah, that kind of makes sense. Under certain circumstances, the impact of the order might not be quite as significant when you’re working in basis vectors.

What is it that happens in the opposite order? If you’re talking about the order in which matrices are applied, I’m pretty sure it’s in the sequence you write them, at least here in Monogame. That’s why we have expressions such as World * View * Projection; that applies the world matrix first, then view, then projection.

I’ve attempted to illustrate once more what your original code was doing, although this is even more sloppy than my earlier one. It’s difficult to perform 3D rotations just “eyeballing” it. But even so, I hope it at least conveys what’s incorrect about doing CreateFromAxisAngle * CreateLookAt.

[willmotil]

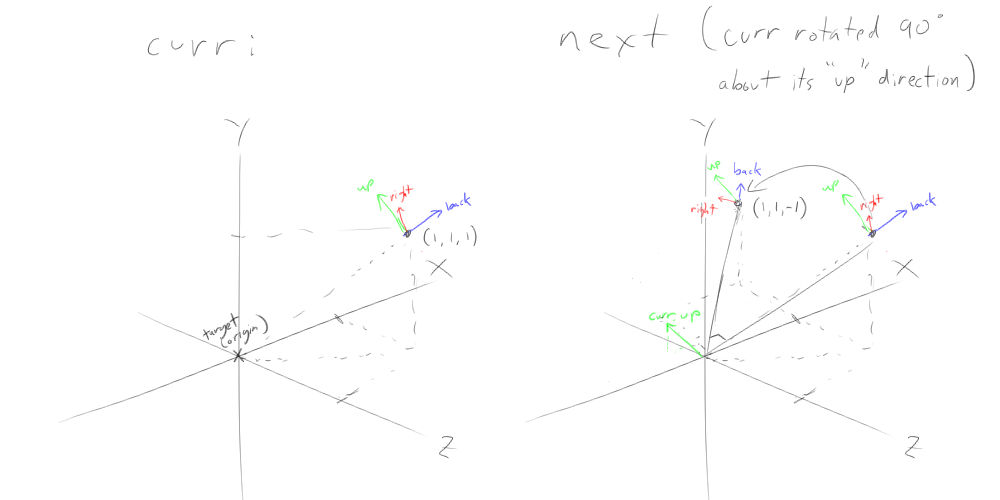
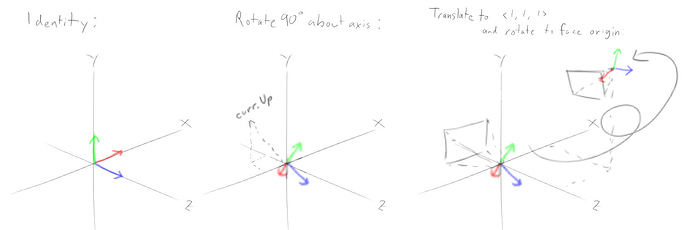
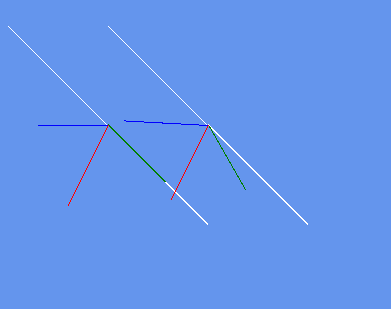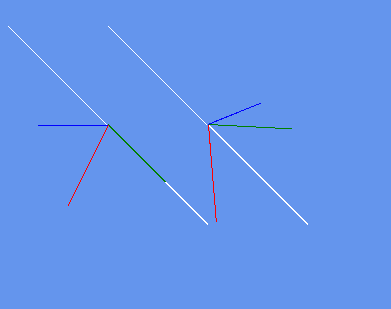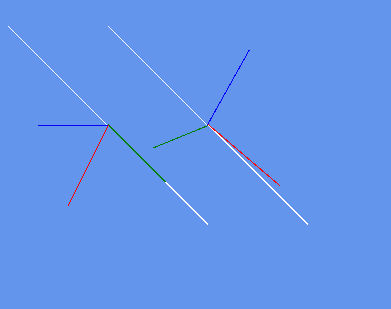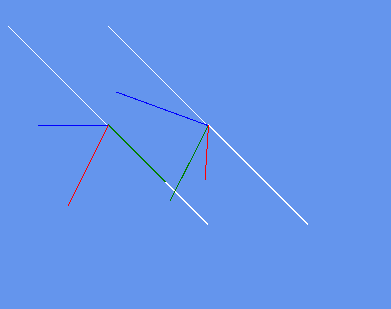
You can use the below class draw line function to view the vectors in the matrix i added a method to draw the matrix orientations as lines at a position on screen you can choose.
Initialize this in load after you created a spritebatch pass it a dot texture you can get one from the class itself or a texture to use for the lines.

Call the following in draw between spritebatch begin end calls.

float t = 0f;
protected override void Draw(GameTime gameTime)
    {
        this.GraphicsDevice.Clear(Color.CornflowerBlue);
        var elapsed = (float)gameTime.ElapsedGameTime.TotalSeconds;
        t += elapsed / 5f;
        if (t > 1f)
            t = 0;

        _spriteBatch.Begin();

        var scale = 50f;
        var offset1 = 100;
        var offset2 = 200;
        var offset3 = 300;

        var axis = Vector3.One;
        DrawHelpers.Draw2DVectorAxis(axis, scale, new Vector2(offset1, offset1));
        DrawHelpers.Draw2DMatrixOrientationWithAxis(Matrix.Identity, axis, scale, new Vector2(offset1, offset1));

        Matrix curr = Matrix.CreateWorld(Vector3.Zero, axis, Vector3.Up);
        DrawHelpers.Draw2DMatrixOrientationWithAxis(curr, axis, scale, new Vector2(offset2, offset1));

        var axis2 = curr.Up;
        DrawHelpers.Draw2DVectorAxis(axis2, scale, new Vector2(offset1, offset2));

        Matrix next = Matrix.CreateFromAxisAngle(axis2, t * 6.28f);
        DrawHelpers.Draw2DMatrixOrientationWithAxis(next, axis2, scale, new Vector2(offset2, offset2));

        Matrix final1 = next * curr;
        var axis3 = final1.Up;
        DrawHelpers.Draw2DMatrixOrientationWithAxis(final1, axis3, scale, new Vector2(offset1, offset3));

        Matrix final2 = curr * next;
        axis3 = final2.Up;
        DrawHelpers.Draw2DMatrixOrientationWithAxis(final2, axis3, scale, new Vector2(offset2, offset3));

        _spriteBatch.End();

        base.Draw(gameTime);
    }

…

public static class DrawHelpers
{
static SpriteBatch spriteBatch;
static Texture2D dot;

/// <summary>
/// Flips atan direction to xna spritebatch rotational alignment defaults to true.
/// </summary>
public static bool SpriteBatchAtan2 = true;

public static void Initialize(SpriteBatch spriteBatch, Texture2D dot)
{
    DrawHelpers.spriteBatch = spriteBatch;
    if(DrawHelpers.dot == null)
        DrawHelpers.dot = dot;
}

public static void DrawRectangleOutline(Rectangle r, int lineThickness, Color c)
{
    DrawSquareBorder(r, lineThickness, c);
}
public static void DrawSquareBorder(Rectangle r, int lineThickness, Color c)
{
    Rectangle TLtoR = new Rectangle(r.Left, r.Top, r.Width, lineThickness);
    Rectangle BLtoR = new Rectangle(r.Left, r.Bottom - lineThickness, r.Width, lineThickness);
    Rectangle LTtoB = new Rectangle(r.Left, r.Top, lineThickness, r.Height);
    Rectangle RTtoB = new Rectangle(r.Right - lineThickness, r.Top, lineThickness, r.Height);
    spriteBatch.Draw(dot, TLtoR, c);
    spriteBatch.Draw(dot, BLtoR, c);
    spriteBatch.Draw(dot, LTtoB, c);
    spriteBatch.Draw(dot, RTtoB, c);
}
public static void DrawBasicLine(Vector2 s, Vector2 e, int thickness, Color linecolor)
{
    Rectangle screendrawrect = new Rectangle((int)s.X, (int)s.Y, thickness, (int)Vector2.Distance(e, s));
    float rot = (float)Atan2Xna(e.X - s.X, e.Y - s.Y);
    spriteBatch.Draw(dot, screendrawrect, new Rectangle(0, 0, 1, 1), linecolor, rot, Vector2.Zero, SpriteEffects.None, 0);
}
public static void DrawBasicPoint(Vector2 p, Color c)
{
    Rectangle screendrawrect = new Rectangle((int)p.X, (int)p.Y, 2, 2);
    spriteBatch.Draw(dot, screendrawrect, new Rectangle(0, 0, 1, 1), c, 0.0f, Vector2.One, SpriteEffects.None, 0);
}
public static float Atan2Xna(float difx, float dify)
{
    if (SpriteBatchAtan2)
        return (float)System.Math.Atan2(difx, dify) * -1f;
    else
        return (float)System.Math.Atan2(difx, dify);
}

public static void Draw2DVectorAxis(Vector3 axis, float scale, Vector2 postion)
{
    var a = new Vector2(axis.X, axis.Y) * scale + postion;
    var n = new Vector2(-axis.X, -axis.Y) * (scale * .25f) + postion;
    DrawBasicLine(postion, a, 1, Color.White);
    DrawBasicLine(postion, n, 1, Color.Gray);
}

public static void Draw2DMatrixOrientation(Matrix m, float scale, Vector2 postion)
{
    var f = new Vector2(m.Forward.X, m.Forward.Y) * scale + postion;
    var r = new Vector2(m.Right.X, m.Right.Y) * scale + postion;
    var u = new Vector2(m.Up.X, m.Up.Y) * scale + postion;

    DrawBasicLine(postion, f, 1, Color.Green);
    DrawBasicLine(postion, u, 1, Color.Red);
    DrawBasicLine(postion, r, 1, Color.Blue);
}


public static void Draw2DMatrixOrientationWithAxis(Matrix m, Vector3 axis, float scale, Vector2 postion)
{
    var f = new Vector2(m.Forward.X, m.Forward.Y) * scale + postion;
    var r = new Vector2(m.Right.X, m.Right.Y) * scale + postion;
    var u = new Vector2(m.Up.X, m.Up.Y) * scale + postion;

    var a = new Vector2(axis.X, axis.Y) * scale + postion;
    var n = new Vector2(-axis.X, -axis.Y) * (scale * .25f) + postion;

    DrawBasicLine(postion, a, 1, Color.White);
    DrawBasicLine(postion, n, 1, Color.Gray);

    DrawBasicLine(postion, f, 1, Color.Green);
    DrawBasicLine(postion, u, 1, Color.Red);
    DrawBasicLine(postion, r, 1, Color.Blue);
}

public static Vector2 MatrixSpriteBatchOut(SpriteBatch spriteBatch, SpriteFont font, Vector2 textPosition, Color col, Matrix m, string name)
{
    var textPos = textPosition;
    spriteBatch.DrawString(font, name, textPos, col);
    textPos.Y += font.LineSpacing;
    float spacing = 110;
    spriteBatch.DrawString(font, " M11: " + m.M11.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M12: " + m.M12.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M13: " + m.M13.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M14: " + m.M14.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " Right ", textPos, col); textPos.X += spacing;
    textPos.X = textPosition.X; textPos.Y += font.LineSpacing;
    spriteBatch.DrawString(font, " M21: " + m.M21.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M22: " + m.M22.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M23: " + m.M23.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M24: " + m.M24.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " Up ", textPos, col); textPos.X += spacing;
    textPos.X = textPosition.X; textPos.Y += font.LineSpacing;
    spriteBatch.DrawString(font, " M31: " + m.M31.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M32: " + m.M32.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M33: " + m.M33.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M34: " + m.M34.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " Forward ", textPos, col); textPos.X += spacing;
    textPos.X = textPosition.X; textPos.Y += font.LineSpacing;
    spriteBatch.DrawString(font, " M41: " + m.M41.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M42: " + m.M42.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M43: " + m.M43.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " M44: " + m.M44.ToString("#0.000"), textPos, col); textPos.X += spacing;
    spriteBatch.DrawString(font, " Position ", textPos, col); textPos.X += spacing;
    textPos.X = textPosition.X; textPos.Y += font.LineSpacing;
    return textPos;
}

public static string MatrixToString(Matrix m, string name)
{
    return
        name +
        "\n  Right: " + m.Right.ToString() + " M41: " + m.M41.ToString() +
        "\n  Up: " + m.Up.ToString() + " M42: " + m.M42.ToString() +
        "\n  Forward: " + m.Forward.ToString() + " M43: " + m.M43.ToString() +
        "\n  Position: " + m.Translation.ToString() + " M44: " + m.M44.ToString();
}
}

[John_Smith]

Which does seem to show the same issue.

Matrix curr = Matrix.CreateLookAt(Vector3.One, Vector3.Zero, Vector3.Up);
Matrix next = Matrix.CreateFromAxisAngle(curr.Up, 1.7f) * curr;

[willmotil]

Ya sorry i edited the above and put the axis in.

hold on ya maybe something funny is going on or im just to tired ill have to double check it later.

[John_Smith]

So this is a gif of what the code is doing and what the nearly identical code in my Transform class is doing. I even checked the source for the axisangle transform and it all seems to be functionally the same apart from column major vs row major.

[ed022]

Did you see my response? It might have pinpointed the point of misunderstanding.

@John_Smith

It actually happens in the opposite order: second * first.

@ed022

What is it that happens in the opposite order? If you’re talking about the order in which matrices are applied, I’m pretty sure it’s in the sequence you write them, at least here in Monogame. That’s why we have expressions such as World * View * Projection; that applies the world matrix first, then view, then projection.

If you assume it occurs in reverse order, then you might be getting different results than you would expect.

[John_Smith]

I might have them messed up but it should still not be skewing the way it is.

[ed022]

Here’s what I tried just now to verify:

Matrix.CreateRotationY(MathHelper.ToRadians(90)) * Matrix.CreateTranslation(Vector3.UnitX)
( -4.371139E-08  0  -1  0 )  
( 0  1  0  0 )  
( 1  0  -4.371139E-08  0 )  
( 1  0  0  1 )
Translation: 1  0  0

Matrix.CreateTranslation(Vector3.UnitX) * Matrix.CreateRotationY(MathHelper.ToRadians(90))
( -4.371139E-08  0  -1  0 )  
( 0  1  0  0 )  
( 1  0  -4.371139E-08  0 )  
( -4.371139E-08  0  -1  1 )
Translation: -4.371139E-08  0  -1

As you can see, the first case rotates first (leaving the translation at the origin), then translates it to the UnitX position. The second case translates to UnitX first, then rotates (about the origin), thereby placing it at -UnitZ. Therefore, it occurs in the order as written.

[John_Smith]

I think you’re right, I didn’t realize changing row->column major switched the order but it makes sense. It also kinda explains why it was corkscrewing instead of going all over the place.

[ed022]

I don’t know exactly what’s happening with regards to row- or column-major - everyone seems to use different conventions for that - all I know is that the order written is the order applied. And yes, that corkscrewing is what I was trying to illustrate in my most recent diagram.

[willmotil]

Sorry i was too tired to reply earlier, hopefully you got this worked out.

To add in most cases axis angle represents a moment of rotation to be multiplied to a orientation matrix (i.e. typically a small amount that is treated as a rate of change).

The order of rotation matters but also the order of multiplication of the vector by the matrix matters as well.

Notice in the final result on the bottom left when we look at the up vector as the new axis if the matrix multiplication isn’t in the right order the up is then in motion so that the axis is in motion.
vs the result on the bottom right.

I edit the previous posted class with the additional methods shown here.

    var scale = 50f;
    var offset1 = 100;
    var offset2 = 200;
    var offset3 = 300;

    var axis = Vector3.One;
    DrawHelpers.Draw2DVectorAxis(axis, scale, new Vector2(offset1, offset1));
    DrawHelpers.Draw2DMatrixOrientationWithAxis(Matrix.Identity, axis, scale, new Vector2(offset1, offset1));

    Matrix curr = Matrix.CreateWorld(Vector3.Zero, axis, Vector3.Up);
    DrawHelpers.Draw2DMatrixOrientationWithAxis(curr, axis, scale, new Vector2(offset2, offset1));

    var axis2 = curr.Up;
    DrawHelpers.Draw2DVectorAxis(axis2, scale, new Vector2(offset1, offset2));

    Matrix next = Matrix.CreateFromAxisAngle(axis2, t * 6.28f);
    DrawHelpers.Draw2DMatrixOrientationWithAxis(next, axis2, scale, new Vector2(offset2, offset2));

    Matrix final1 = next * curr;
    var axis3 = final1.Up;
    DrawHelpers.Draw2DMatrixOrientationWithAxis(final1, axis3, scale, new Vector2(offset1, offset3));

    Matrix final2 = curr * next;
    axis3 = final2.Up;
    DrawHelpers.Draw2DMatrixOrientationWithAxis(final2, axis3, scale, new Vector2(offset2, offset3));

Also you may wish to consider what rotation vector (forward up or right) the Axis parameter itself represents, when it is rotated by a amount of radians. In the AxisAngle function