Ya i probably didn’t write that little example intuitively i have always been a poor writer and the gif i had up is deleted by photobucket which really illustrated the idea. It’s pretty simple though hard to explain…
Ill try to state it succinctly and directly. For narrow phase polygon surface collision detection.
.
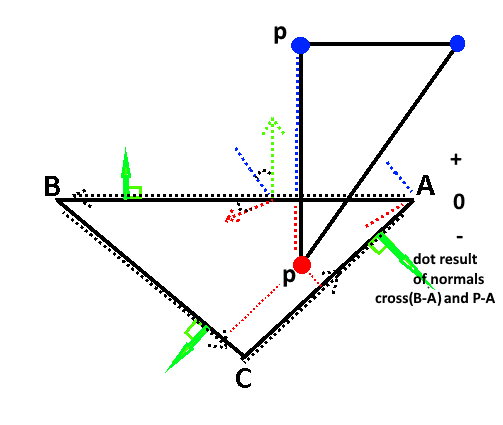
If you have two points A and B (in 2d this is a line and it can be considered equivalent to a plane in 3d).
B-A is a direction vector with A as a origin.
The direction vector and point A together can be considered to be a Ray.
When the direction vector is first normalized and then a perpendicular normal is found to it.
That normal is then said to be a Surface Normal as it is perpendicular to the plane, (which as previously stated in 2d is the line).
So in 2d it is a Surface Normal that is perpendicular to the polygon line AB.
A surface normal has one of two possible orientations to a plane which in 2D is the line.
In or Out.
This correlates directly to winding clockwise or counter clockwise.
Which in 2D is directly determined by selecting … B-A or A-B for the initial direction vector.
This in 2D is simplified to being a Left cross or Right cross product (in relation to the direction of the vector formed from a-b or b-a).
All three of these descriptions are synonymous.
Once this surface normal is known then any vertice of a opposing polygon, to be consider for collision with the surface of the initial polygon. Can be compared to find the directionallity between the two normals in scalar form. I.E. to get a In or Out result in the form of a floating point value.
Some secondary polygons point (denoted as) C, to the line A B of the first polygon.
Can be made into a direction vector by C - A
This is the same point A we used as the subtractor earlier for B - A.
The result is normalized.
These two normals that we have now found, the Surface Normal and the new Direction Vector
These two can be doted against each other to determine what side of the line a point is on.
This gives a result that has one of three possible signs that have a implicit meaning for collision.
A result of
0 is ON the line. (perpendicular normal pair)
-1 INside the line. (opposing normal pair)
+1 OUTside the line. (parallel normal pair)
Knowing if a vertice of a polygon is inside or outside of a line is rather meaningless in most cases however knowing if a opposing polygons vertice is inside of 3 lines of a triangle is knowing if a collision has occurred and then some.
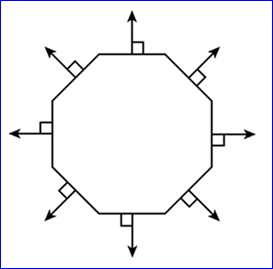
So this process must be repeated for all 3 lines of a triangle or all the lines of a Convex polygon.
Concave polygons must be subdivided into 2 or more distinct groups of checks that are analogous to, a Concave equivalent of the original convex polygon.
The primary thing you test for is failure such that success is extensively not failing the tests.
Tthe dot and cross product can be combined in 2D. The cross and dot for B-A is shown below.
public static bool HasPointCrossedLine2d(Vector2 start, Vector2 end, Vector2 collisionPoint)
{
Vector2 B = (end - start);
Vector2 C = (collisionPoint - start);
// Cross right and dot
float sign = C.X * -B.Y + C.Y * B.X;
// We only need the signed result.
if (sign > 0.0f)
return true;
else
return false;
}
So in summation.
For a 2d triangle with points C B A you can then see that B-A forms a line.
All polygons are composed of vertices that form lines.
Two triangles can be checked for intersections to vertices extremely cheap for two triangles with 100% accuracy in 6 checks.
via … float sign = A.X * -B.Y + A.Y * B.X;
The more complex the polygon geometry the more checks are required however other strategys can be employed to find a faster fail.
This technique is invariant under rotation.
A surface normal can be generated just like a lighting normal in a 3d calculation and use for collision and culling.
In fact that is exactly what this is in 2d and exactly what the gpu does in 3d (except with the 3d vector calculation) to determine backface or front face removal when the render state for culling is set.
This is just the 2d equivalent which is both simpler faster and gleems just as much information as 3d.
You can find reflection refraction and perform all familiar light normal operations in this context for collisions.
To say you can have a bullet or vertex hit your polygons surface and calculate the angle which it will be reflected off similarly to the way you find the angle for reflection of light on the surface of a triangle in 3d ect.
This is a very very old technique now and has been around since the 70’s and even in games in the 80’s.
Both complex ideologically and simple mathematically it is a fundamental concept for gpu’s and accurate surface collision detection in the narrow phase.
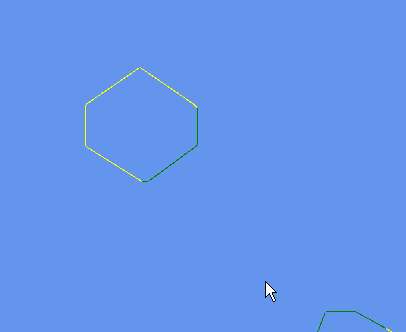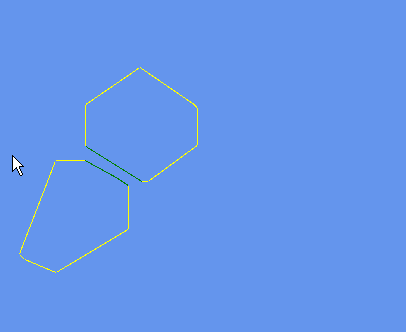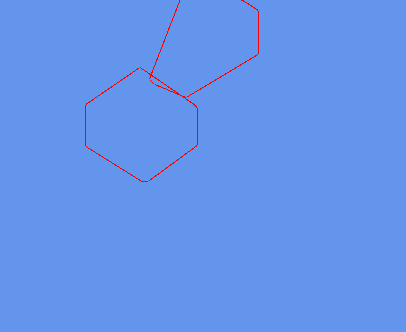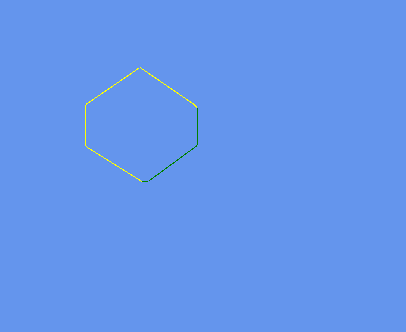
// standalone game1 test.
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using Microsoft.Xna.Framework;
using Microsoft.Xna.Framework.Graphics;
using Microsoft.Xna.Framework.Input;
namespace NarrowPhasePolygonCollision
{
public class Game1 : Game
{
public static GraphicsDeviceManager graphics;
public static SpriteBatch spriteBatch;
public static Texture2D dotTexture;
public float autoRotZ = 0;
Matrix polyWorld = Matrix.Identity;
Matrix polyWorld2 = Matrix.Identity;
public Vector2[] polygonPoints = new Vector2[]
{
new Vector2( 120,33),
new Vector2( 120,76),
new Vector2( 48,119),
new Vector2( 17,106),
new Vector2( 12,101),
new Vector2( 48,8),
new Vector2( 77,8),
new Vector2( 108,25)
};
public Vector2[] polygonPoints2 = new Vector2[]
{
new Vector2( 122,44),
new Vector2( 122,81),
new Vector2( 73,117),
new Vector2( 67,117),
new Vector2( 11,82),
new Vector2( 11,41),
new Vector2( 65,4),
new Vector2( 119,41)
};
//public Vector2[] polygonPoints3 = new Vector2[]
//{
// new Vector2( 0,0),
// new Vector2( 100, 00),
// new Vector2( 100,100),
// new Vector2( 00, 100)
//};
public Game1()
{
graphics = new GraphicsDeviceManager(this);
Content.RootDirectory = "Content";
graphics.GraphicsProfile = GraphicsProfile.HiDef;
IsMouseVisible = true;
Window.AllowUserResizing = true;
graphics.PreferredBackBufferWidth = 800;
graphics.PreferredBackBufferHeight = 600;
}
protected override void Initialize()
{
base.Initialize();
}
protected override void LoadContent()
{
spriteBatch = new SpriteBatch(GraphicsDevice);
dotTexture = TextureDotCreate(GraphicsDevice);
polyWorld.Translation = new Vector3(100, 100, 0);
polyWorld2.Translation = new Vector3(100, 300, 0);
Window.ClientSizeChanged += OnResize;
}
public void OnResize(Object sender, EventArgs e)
{
}
protected override void UnloadContent()
{
dotTexture.Dispose();
}
protected override void Update(GameTime gameTime)
{
if (GamePad.GetState(PlayerIndex.One).Buttons.Back == ButtonState.Pressed || Keyboard.GetState().IsKeyDown(Keys.Escape))
Exit();
if (Mouse.GetState().LeftButton == ButtonState.Pressed)
autoRotZ += gameTime.ElapsedGameTime.TotalSeconds.ToFloat() * 1f;
if (autoRotZ >= 6.28f)
autoRotZ = 0;
var p = Mouse.GetState().Position;
polyWorld.Translation = new Vector3(p.X, p.Y, 0);
polyWorld2 = Matrix.CreateRotationZ(autoRotZ);
polyWorld2.Translation = new Vector3(200, 200, 0);
base.Update(gameTime);
}
protected override void Draw(GameTime gameTime)
{
GraphicsDevice.Clear(Color.CornflowerBlue);
int w = GraphicsDevice.Viewport.Width;
int h = GraphicsDevice.Viewport.Height;
spriteBatch.Begin();
TestCollisionAndDrawPolygonLineResultsIndividually(polygonPoints, polyWorld, polygonPoints2, polyWorld2);
spriteBatch.End();
base.Draw(gameTime);
}
/// <summary>
/// 2d narrow phase point to plane collision.
/// </summary>
public static bool HasPointCrossedLine2d(Vector2 start, Vector2 end, Vector2 collisionPoint)
{
Vector2 n = (end - start);
Vector2 n2 = (collisionPoint - start);
if (n2.X * -n.Y + n2.Y * n.X > 0.0f) // Cross right and dot. We only need the signed result.
return true;
else
return false;
}
/// <summary>
/// Checks if a 2d convex polygon with a arbitrary number of vertices has collided with another by vertex comparison.
/// </summary>
public bool TestPolygonSurfaceCollision(Vector2[] polygonPointsA, Matrix worldA, Vector2[] polygonPointsB, Matrix worldB)
{
// test polygon 1 against polygon 2.
for (int j = 0; j < polygonPointsB.Length; j++)
{
int checks = 0;
for (int i = 0; i < polygonPointsA.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonPointsA.Length)
i2 = 0;
if (HasPointCrossedLine2d(Vector2.Transform(polygonPointsA[i], worldA), Vector2.Transform(polygonPointsA[i2], worldA), Vector2.Transform(polygonPointsB[j], worldB)))
checks++;
if (checks >= polygonPointsA.Length )
return true;
}
}
// test polygon 2 against polygon1.
for (int j = 0; j < polygonPointsA.Length; j++)
{
int checks = 0;
for (int i = 0; i < polygonPointsB.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonPointsB.Length)
i2 = 0;
if (HasPointCrossedLine2d(Vector2.Transform(polygonPointsB[i], worldB), Vector2.Transform(polygonPointsB[i2], worldB), Vector2.Transform(polygonPointsA[j], worldA)))
checks++;
if (checks >= polygonPointsB.Length )
return true;
}
}
return false;
}
/// <summary>
/// This is all wastefully to visualize what is occuring piece wise per line.
/// </summary>
public void TestCollisionAndDrawPolygonLineResultsIndividually(Vector2[] polygonVectorsA, Matrix worldA, Vector2[] polygonVectorsB, Matrix worldB)
{
// For illustration purposes well redraw this all red if a collision has occured.
// This time however we must check each point proper against all the collision surfaces of a convex polygon to make sure it is contained.
//
if (TestPolygonSurfaceCollision(polygonVectorsA, polyWorld, polygonPoints2, polyWorld2))
{
// draw polygons lines
for (int i = 0; i < polygonVectorsA.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonVectorsA.Length)
i2 = 0;
var A = Vector2.Transform(polygonVectorsA[i], polyWorld);
var B = Vector2.Transform(polygonVectorsA[i2], polyWorld);
DrawBasicLine(A, B, 1, Color.Red, 0);
}
for (int i = 0; i < polygonPoints2.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonPoints2.Length)
i2 = 0;
var A = Vector2.Transform(polygonPoints2[i], polyWorld2);
var B = Vector2.Transform(polygonPoints2[i2], polyWorld2);
DrawBasicLine(A, B, 1, Color.Red, 0);
}
}
else // is not colliding
{
// This will display if any opposing polygons points are inside each line this does not nessecariily mean there is a collision.
// If so draw a yellow line
// else draw a green line.
for (int i = 0; i < polygonVectorsA.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonVectorsA.Length)
i2 = 0;
var A = Vector2.Transform(polygonVectorsA[i], worldA);
var B = Vector2.Transform(polygonVectorsA[i2], worldA);
int checks = 0;
for (int j = 0; j < polygonVectorsB.Length; j++)
{
var C = Vector2.Transform(polygonVectorsB[j], worldB);
if (HasPointCrossedLine2d(A, B, C))
checks++;
}
if (checks > 0)
DrawBasicLine(A, B, 1, Color.Yellow, 0);
else
DrawBasicLine(A, B, 1, Color.Green, 0);
}
for (int i = 0; i < polygonVectorsB.Length; i++)
{
int i2 = i + 1;
if (i2 == polygonVectorsB.Length)
i2 = 0;
var A = Vector2.Transform(polygonVectorsB[i], worldB);
var B = Vector2.Transform(polygonVectorsB[i2], worldB);
int checks = 0;
for (int j = 0; j < polygonVectorsA.Length; j++)
{
var C = Vector2.Transform(polygonVectorsA[j], worldA);
if (HasPointCrossedLine2d(A, B, C))
checks++;
}
if (checks > 0)
DrawBasicLine(A, B, 1, Color.Yellow, 0);
else
DrawBasicLine(A, B, 1, Color.Green, 0);
}
}
}
public static void DrawBasicLine(Vector2 s, Vector2 e, int thickness, Color linecolor, float rot)
{
Rectangle screendrawrect = new Rectangle((int)s.X, (int)s.Y, thickness, (int)Vector2.Distance(s, e));
spriteBatch.Draw(dotTexture, screendrawrect, new Rectangle(0, 0, 1, 1), linecolor, ((float)Math.Atan2(e.X - s.X, e.Y - s.Y) * -1f) + rot, Vector2.Zero, SpriteEffects.None, 0);
}
public static Texture2D TextureDotCreate(GraphicsDevice device)
{
Color[] data = new Color[1];
data[0] = new Color(255, 255, 255, 255);
Texture2D tex = new Texture2D(device, 1, 1);
tex.SetData<Color>(data);
return tex;
}
}
}
In 3d it would look like so…
Though i didn’t set up a test for this probably bugged since i typed it straight out.
/// <summary>
/// 3d narrow phase point to plane collision.
/// </summary>
public static bool HasPointCrossedPlane(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 collisionPoint)
{
Vector3 n = Vector3.Cross(p1 - p0, p2 - p0);
Vector3 n2 = (collisionPoint - p0);
if (Vector3.Dot(n,n2) > 0.0f) // Cross right and dot. We only need the signed result.
return true;
else
return false;
}
/// <summary>
/// Checks if a 3d convex polygon with a arbitrary number of vertices has collided with another by vertex comparison.
/// </summary>
public bool TestConvexPolyhedronSurfaceCollision(VertexPositionColor[] polygonPointsA, int[] indicesA, Matrix worldA, VertexPositionColor[] polygonPointsB, int[] indicesB, Matrix worldB)
{
// test polygon 1 against polygon 2.
for (int j = 0; j < polygonPointsB.Length; j++)
{
int checks = 0;
for (int i = 0; i < indicesA.Length/3; i+=3)
{
int i1 = i + 1;
int i2 = i + 2;
var p0 = polygonPointsA[i].Position;
var p1 = polygonPointsA[i1].Position;
var p2 = polygonPointsA[i2].Position;
if (HasPointCrossedPlane(Vector3.Transform(p0, worldA), Vector3.Transform(p1, worldA), Vector3.Transform(p2, worldA), Vector3.Transform(polygonPointsB[j].Position, worldB)) )
checks++;
if (checks >= indicesA.Length / 3)
return true;
}
}
// test polygon 2 against polygon1.
for (int j = 0; j < polygonPointsA.Length; j++)
{
int checks = 0;
for (int i = 0; i < indicesB.Length / 3; i += 3)
{
int i1 = i + 1;
int i2 = i + 2;
var p0 = polygonPointsB[i].Position;
var p1 = polygonPointsB[i1].Position;
var p2 = polygonPointsB[i2].Position;
if (HasPointCrossedPlane(Vector3.Transform(p0, worldB), Vector3.Transform(p1, worldB), Vector3.Transform(p2, worldB), Vector3.Transform(polygonPointsA[j].Position, worldA)))
checks++;
if (checks >= indicesB.Length / 3)
return true;
}
}
return false;
}








