It seems like this should be eazy but im feeling brain dead today.
I have points a b c that form a triangle i know points A B C form a right triangle based on point B
I know the position of point B and C and i know a radian theta angle of 1.0f exists formed from a angle create from A to B and A to C
I need to know from this were A.x is since i already know A.y = 0;
nvm i think i figured it out.
float w = GraphicsDevice.Viewport.Width;
float h = GraphicsDevice.Viewport.Height;
float hw = w / 2;
float hh = h / 2;
var rads = 1.0f;
var p2 = new Vector2(w, hh);
var p3 = new Vector2(w, h);
float dist2to3 = Vector2.Distance(p2, p3);
var tanRads = (float)Math.Tan(rads);
float solvedX = dist2to3 / tanRads;
var p1 = new Vector2(w - solvedX , hh);
Unfortunately this didn’t solve my real problem so now its worse ackk.
Math: SOH CAH TOA
Yah, that answer looks right by my math. Does this account for differences in quadrants I’m wondering - or is the real problem unrelated? Like I know I use tan2 cuz it accounts for that. EDIT - Silly me, I just realized it would only ever be in one quadrant.
Ya that previously was actually wrong but by concept which is why it wasn’t working.
This is a better description or solution to the problem.
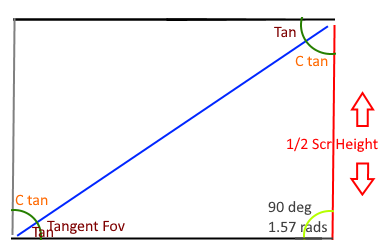
So this is for finding a perspective fov camera position distance that aligns to a orthographic width and height. As you know the aspect ratio is defined in the perspective fov calculation and the orthographic has a width height so they at some fov angle line up, provided the camera is positioned properly.
So the question i was wondering is how do you find that point were the camera must be placed in relation to the orthographic spritebatch drawing xy plane aka position 0 z depth. Then how far back does a perspective camera with a abitrary fov have to be to match that planes width and height. Aka how to calculate that value…
Anyways so after a bit of thinking i figured it out.
It’s the half co-tangent of the perspective field of view and then the half height of the orthographic screen multiplied then the result has the be negated as well.
var dist = -((1f / (float)Math.Tan(style._fov / 2)) * (device.Viewport.Height / 2));
This is then feed to the camera matrix along with the half width and half height of the screen as the cameras position to pull the position back as spritebatch looks into the positive plane.
if (style == CameraStylePerspectiveSpriteBatch)
{
var dist = -((1f / (float)Math.Tan(style._fov / 2)) * (device.Viewport.Height / 2));
pos = new Vector3(device.Viewport.Width / 2, device.Viewport.Height / 2, dist);
target = new Vector3(0 , 0, 1) + pos;
}
TransformCamera(pos, target, up);
// the above essentially uses create world then the view is just the Matrix.Invert.
// One additional note here is the UP vector is actually Vector3.Down in this case.
The outline in black is using the default spritebatch begin and drawing the rectangles.
The textured ones are using a basic effect or custom effect were i set the view position and projection as perspective. The motion is to show they are aligned.
The projection matrix has a arbitrary field of view the near and far plane don’t matter much as long as the sum of the near far isn’t less then the dist value.
_projection = MatrixHelpers.DXCreatePerspectiveFieldOfViewRHLH(fieldOfView, _device.Viewport.AspectRatio, currentCameraStyle._near, currentCameraStyle._far, true);
The following projection matrix is used which basically is the same one as monogames Matrix.CreatePerspectiveFov
public static Matrix DXCreatePerspectiveFieldOfViewRHLH(float fieldOfView, float aspectRatio, float nearPlaneDistance, float farPlaneDistance, bool isRightHanded)
{
/* RH
m11= xscale m12= 0 m13= 0 m14= 0
m21= 0 m22= yscale m23= 0 m24= 0
m31= 0 0 m33= f/(f-n) m34= -1
m41= 0 m42= 0 m43= n*f/(n-f) m44= 0
where:
yScale = cot(fovY/2)
xScale = yScale / aspect ratio
*/
if ((fieldOfView <= 0f) || (fieldOfView >= 3.141593f))
{
throw new ArgumentException("fieldOfView <= 0 or >= PI");
}
Matrix result = new Matrix();
float yscale = 1f / ((float)Math.Tan((double)(fieldOfView * 0.5f)));
float xscale = yscale / aspectRatio;
result.M11 = xscale;
result.M12 = result.M13 = result.M14 = 0;
result.M22 = yscale;
result.M21 = result.M23 = result.M24 = 0;
result.M31 = result.M32 = 0f;
if (isRightHanded)
{
result.M33 = farPlaneDistance / (nearPlaneDistance - farPlaneDistance);
result.M34 = -1;
result.M43 = (nearPlaneDistance * farPlaneDistance) / (nearPlaneDistance - farPlaneDistance);
}
else
{
result.M33 = farPlaneDistance / (farPlaneDistance - nearPlaneDistance);
result.M34 = 1;
result.M43 = (-nearPlaneDistance * farPlaneDistance) / (farPlaneDistance - nearPlaneDistance);
}
result.M41 = result.M42 = result.M44 = 0;
return result;
}
Later on im gonna try to just stick that into the projection matrix so the view matrix doesn’t need to be positioned at all, im not sure that is possible it seems simple enough but i haven’t tried yet maybe tommorow ill try.