I spent about a good 6 hours or more attempting to solve a problem that you normally have to make a ton of separate 3d quads many times over to solve.
A perspective spritebatch like call on a single quad were i don’t change the vertices positions. I wanted to make a straight 3d draw call that allows a single quad to be drawn in 3d like fashion via a rectangle and which doesn’t alter the vertices themselves. Were it is done via matrices and calculation !
Something like a 2d spritebatch with 3d perspective projection when you move in depth or want to rotate the rectangle into the z plane.
DrawQuad(Texture2D t, Rectangle dest, float Xrotation)
were really i can rotate in x y or z and use a rectangle to plot the position.
I wasn’t sure i could figure out how to do it, but it turns out i did and a little more to boot. I really wanted to figure out how to do it within a perspective projection matrix so that while the z depth was zero it would be orthographic and spritebatch like. Im sure i can think of some cool uses for this later…
The only cavet to this so far is when you draw under this you need a special view matrix. You also need to update the projection matrix if the screen size changed.
so here is the code …
first thing is to create the view matrix as if it is 2d and wrap the create fov perspective projection matrix.
public void loadCreateProjectionViewOrtho()
{
CreateFovProjectionMatrix(90, .5f, 2000f);
CreateUnitView();
}
public void CreateUnitView()
{
viewOrth = Matrix.CreateLookAt(Vector3.Backward * 1f, Vector3.Forward * 0f, Vector3.Up);
}
Now that the potatoes are out of the way, here is the meat of it.
I wrapped up the projection matrix creation so i can create and keep a few extra values to align the draw calls that take rectangles. The crucial math is in the below four found values.
halfFovTangent, frustrumAspectCoefficient, posMultiplier, whMultiplier.
These are used to invert some of the main calculations of a fov perspective create method. If you look inside that method you see sort of how i found the inverses. These are applied in the draw call.
float sx = dest.X * +posMultiplier + (-1f * halfFovTangent * aspect);
float sy = dest.Y * -posMultiplier + (+1f * halfFovTangent);
float sw = dest.Width * whMultiplier;
float sh = dest.Height * whMultiplier;
They are used to translate a quad via translate and scaling to be equivalent to a rectangle under a varying fov near and far plane. I digress.
Matrix viewOrth;
Matrix projection;
float fov;
float aspect;
float halfFovTangent;
float frustrumAspectCoefficient;
float posMultiplier;
float whMultiplier;
public void CreateFovProjectionMatrix(float fovDegrees, float near, float far)
{
float ToRads = (float)(Math.PI * 2.0d) / 360f;
var w = GraphicsDevice.PresentationParameters.BackBufferWidth;
var h = GraphicsDevice.PresentationParameters.BackBufferHeight;
aspect = (float)(w) / (float)(h);
fov = ToRads * fovDegrees;
halfFovTangent = (float)Math.Tan((double)(fov * 0.5f));
frustrumAspectCoefficient = 1f / ((1f / halfFovTangent) / aspect);
posMultiplier = (frustrumAspectCoefficient / h);
whMultiplier = 1f / (h * halfFovTangent);
projection = Matrix.CreatePerspectiveFieldOfView(fov, aspect, near, far);
}
And with these values calculated i can draw with a rectangle in perspective projection.
public void DrawQuad(Texture2D t, Rectangle dest, float Xrotation)
{
float sx = dest.X * +posMultiplier + (-1f * halfFovTangent * aspect);
float sy = dest.Y * -posMultiplier + (+1f * halfFovTangent);
float sw = dest.Width * whMultiplier;
float sh = dest.Height * whMultiplier;
Matrix world = Matrix.Identity * Matrix.CreateRotationX(Xrotation) * Matrix.CreateScale(sw, sh, 1f);
world.Translation = new Vector3(sx, sy, 0f);
Matrix wvp = world * viewOrth * projection;
GraphicsDevice.RasterizerState = RasterizerState.CullNone;
myeffect.Parameters["lightDir"].SetValue(Vector3.Normalize(obj_Light.Forward));
myeffect.Parameters["TextureA"].SetValue(t);
myeffect.Parameters["gworld"].SetValue(world);
myeffect.Parameters["gworldviewprojection"].SetValue(wvp);
myeffect.CurrentTechnique = myeffect.Techniques["QuadDraw"];
foreach (EffectPass pass in myeffect.CurrentTechnique.Passes)
{
pass.Apply();
pvs.DrawUserIndexPrimitiveQuad(GraphicsDevice);
}
}
When the sprite is not rotated the sprite can be drawn as a rectangle.
.
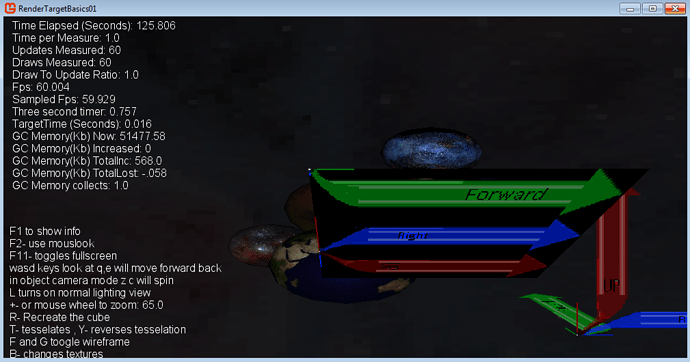
When it is however, it abides by perspective projection. So in the below image the quad is rotated on its X axis. Two of the vertices abide by spritebatch orthographic and two are prospectively influenced as they dip into the z plane.
In the below image the top line of the square sprite is the rectangles width
the quad used here is made so the top left is the rotational origin.
private void CreateQuad()
{
//
// // 0 2
// // LT --- RT
// // | / |
// // |1 / | 3
// // LB --- RB
//
float z = 0.0f;
float adjustmentX = .5f;
float adjustmentY = -.5f;
float scale = 2f; // scale 2 and matrix identity passed straight thru is litterally orthographic
//_vertices = new VertexPositionNormalTexture[4];
vertices_A = new VertexPositionNormalColorUv[4];
vertices_A[0].Position = new Vector3((adjustmentX - 0.5f) * scale, (adjustmentY - 0.5f) * scale, z);
vertices_A[0].Normal = Vector3.Backward;
vertices_A[0].Color = Color.White;
vertices_A[0].TextureCoordinateA = new Vector2(0f, 1f);
vertices_A[1].Position = new Vector3((adjustmentX - 0.5f) * scale, (adjustmentY + 0.5f) * scale, z);
vertices_A[1].Normal = Vector3.Backward;
vertices_A[1].Color = Color.White;
vertices_A[1].TextureCoordinateA = new Vector2(0f, 0f);
vertices_A[2].Position = new Vector3((adjustmentX + 0.5f) * scale, (adjustmentY - 0.5f) * scale, z);
vertices_A[2].Normal = Vector3.Backward;
vertices_A[2].Color = Color.White;
vertices_A[2].TextureCoordinateA = new Vector2(1f, 1f);
vertices_A[3].Position = new Vector3((adjustmentX + 0.5f) * scale, (adjustmentY + 0.5f) * scale, z);
vertices_A[3].Normal = Vector3.Backward;
vertices_A[3].Color = Color.White;
vertices_A[3].TextureCoordinateA = new Vector2(1f, 0f);
indices_A = new int[6];
indices_A[0] = 0;
indices_A[1] = 1;
indices_A[2] = 2;
indices_A[3] = 2;
indices_A[4] = 1;
indices_A[5] = 3;
}
In summation this sort of technique allows for drawing super cool top down levels that have real perspective depth while placing everything with spritebatch like positioning calls. The view matrix can still pan along x or y and preserve the alignment the projection matrix can still alter its fov. Its really in 3d and lighting and everything will still work.
This also holds the prospect for potentially instancing a spritebatch like set of calls that take rectangles for a world.
So its pretty neat.
This is the road less traveled i wanted to see, how it would work, and if it could. It can and so here is the proof,. i wanted to post it because figuring out the math, was a bitch