Here is a unit in my game moving in column formation:
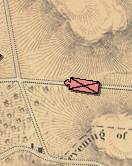
Now, when a user wants to change the unit from column to line formation it should look like this:

The key things to remember here are the stored location of the unit is where the arrowhead is. That is to say, the unit location X,Y for the unit in column formation (top photo) is at the base of the arrowhead. The unit location X,Y for the bottom unit in line formation is between the two arrowheads where they connect with the unit.
Previously, you guys helped me out with rotating these units and calculating their new corners and using this for unit collision detection.
This code returns the 4 corners of a rotated unit:
UnitRect = CalculateActualRect(TheUnit, TheUnit.Location);
Vector2[] corners = CalculateCorners(UnitRect, (float)TheUnit.Facing);
public static Rectangle CalculateActualRect(MATEUnit TheUnit, PointI Location)
{
Rectangle ActualCorners = new Rectangle();
// We have to calculate the actual X1,Y1 X2,Y2 of the unit rect
// Taking into consideration unit type
// and unit formation
// Also, scale by PieceSize
if (TheUnit.Type == (int)UnitTypes.Supplies ||
TheUnit.Type == (int)UnitTypes.HeadQuarters ||
TheUnit.Type == (int)UnitTypes.Artillery ||
TheUnit.Type == (int)UnitTypes.HorseArtillery)
{
if (TheUnit.Formation == Formations.Column ||
TheUnit.Formation == Formations.MeleeColumn)
{
// These are UNSCALED icon sizes
// 26 x 44 including arrows
// 26 x 33 without arrows
ActualCorners = new Rectangle(TheUnit.Location.X - (int)(13 * PieceSize), TheUnit.Location.Y, (int)(26 * PieceSize), (int)(44 * PieceSize));
} // column formation
else // line formation
{
// 44 x 36 including arrows
// 44 x 25 without arrows
ActualCorners = new Rectangle(TheUnit.Location.X - (int)(22 * PieceSize), TheUnit.Location.Y, (int)(44 * PieceSize), (int)(36 * PieceSize));
}
} // small unit
else // large unit
{
if (TheUnit.Formation == Formations.Column ||
TheUnit.Formation == Formations.MeleeColumn)
{
// 26 x 71 including arrows
// 26 x 60 without arrows
ActualCorners = new Rectangle(TheUnit.Location.X - (int)(13 * PieceSize), TheUnit.Location.Y, (int)(36 * PieceSize), (int)(71 * PieceSize));
} // column formation
else // line formation
{
// 62 x 38 including arrows
// 62 x 27 without arrows
ActualCorners = new Rectangle(TheUnit.Location.X - (int)(31 * PieceSize), TheUnit.Location.Y, (int)(62 * PieceSize), (int)(38 * PieceSize));
}
} // large unit
return ActualCorners;
} // CalculateActualRect
private static Vector2[] CalculateCorners(Rectangle rect, float angle)
{
// Calculate the four corners of the rectangle
Vector2[] corners = new Vector2[4];
corners[0] = new Vector2(rect.Left, rect.Top);
corners[1] = new Vector2(rect.Right, rect.Top);
corners[2] = new Vector2(rect.Right, rect.Bottom);
corners[3] = new Vector2(rect.Left, rect.Bottom);
// Rotate the corners around the center of the rectangle
// AHA! Our units don't rotate around the center!
//Vector2 center = new Vector2(rect.Center.X, rect.Center.Y);
Vector2 center = new Vector2(rect.Center.X, rect.Top + 5);
for (int i = 0; i < corners.Length; i++)
{
corners[i] = RotatePoint(corners[i], center, angle);
}
return corners;
}
private static Vector2 RotatePoint(Vector2 point, Vector2 center, float angle)
{
// Rotate a point around another point by a given angle
float sin = (float)Math.Sin(angle);
float cos = (float)Math.Cos(angle);
Vector2 translated = new Vector2(point.X - center.X, point.Y - center.Y);
Vector2 rotated = new Vector2(
translated.X * cos - translated.Y * sin,
translated.X * sin + translated.Y * cos);
return new Vector2(rotated.X + center.X, rotated.Y + center.Y);
}
What I need to do now is calculate the new Location Point (X,Y) of the unit after it has been changed from line to column formation or from column to line formation. Note that the unit occupies the exact same space, it’s just that the Point from where the unit is drawn is changed.
Hopefully, these two images will explain:
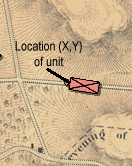
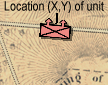
So, the question is: given the above methods and info, how do I calculate the new Location (X,Y) point after a unit is changed from column to line formation (or vice versa)?
Or, to put another way, what is the new point (X,Y) that will cause the unit to be drawn occupying the exact same space on the map (arrowheads don’t count) when the unit changes from column to line formation?