I really need another set of eyes on this problem. I’m going around in circles and I really appreciate everybody’s help. I’m going to lay out all the steps and methods. Sorry for the long post.
First, because of a decision made by my coding partner who isn’t using MonoGame, but WPF, the center of our sprites aren’t where they should be. The ‘point’ of a sprite, the location, is actually the tip of the arrowhead. This has caused a ton of problems.
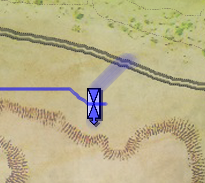
Consequently, I have to go through a bunch of steps to find the true rectangle of a unit. So, as we can see from this screen cap that outlines the true rects of a unit, we can determine the actual location of the unit:
So, given the location of the unit (and the unit type) we have this code:
public static Rectangle CalculateActualRect(MATEUnit TheUnit, PointI Location)
{
Rectangle ActualCorners = new Rectangle();
// We have to calculate the actual X1,Y1 X2,Y2 of the unit rect
// Taking into consideration unit type
// and unit formation
// Also, scale by PieceSize
if (TheUnit.Type == (int)UnitTypes.Supplies ||
TheUnit.Type == (int)UnitTypes.HeadQuarters ||
TheUnit.Type == (int)UnitTypes.Artillery ||
TheUnit.Type == (int)UnitTypes.HorseArtillery)
{
if (TheUnit.Formation == Formations.Column ||
TheUnit.Formation == Formations.MeleeColumn)
{
// These are UNSCALED icon sizes
// 24 x 55 including arrows
// 24 x 44 without arrows
ActualCorners = new Rectangle(Location.X - (int)(12 * PieceSize), (int)(Location.Y + (UnscaledArrowheads * PieceSize)), (int)(24 * PieceSize), (int)(55 * PieceSize) - (int)(UnscaledArrowheads * PieceSize));
} // column formation
else // line formation
{
// 44 x 38 including arrows
// 44 x 27 without arrows
ActualCorners = new Rectangle(Location.X - (int)((44 / 2) * PieceSize), Location.Y + (int)(UnscaledArrowheads * PieceSize), (int)(44 * PieceSize), (int)(38 * PieceSize) - (int)(UnscaledArrowheads * PieceSize));
}
} // small unit
else // large unit
{
if (TheUnit.Formation == Formations.Column ||
TheUnit.Formation == Formations.MeleeColumn)
{
// 27 x 74 including arrows
// 27 x 62 without arrows
ActualCorners = new Rectangle(Location.X - (int)((27 / 2) * PieceSize), (int)(Location.Y + (UnscaledArrowheads * PieceSize)), (int)(27 * PieceSize), (int)((74 * PieceSize) - (UnscaledArrowheads * PieceSize)));
} // column formation
else // line formation
{
// 62 x 38 including arrows
// 62 x 27 without arrows
ActualCorners = new Rectangle(Location.X - (int)(31 * PieceSize), Location.Y + (int)(UnscaledArrowheads * PieceSize), (int)(62 * PieceSize), (int)(38 * PieceSize) - (int)(UnscaledArrowheads * PieceSize));
}
} // large unit
return ActualCorners;
} // CalculateActualRect
private static Vector2[] CalculateCorners(Rectangle rect, float angle)
{
// Calculate the four corners of the rectangle
Vector2[] corners = new Vector2[4];
corners[0] = new Vector2(rect.Left, rect.Top);
corners[1] = new Vector2(rect.Right, rect.Top);
corners[2] = new Vector2(rect.Right, rect.Bottom);
corners[3] = new Vector2(rect.Left, rect.Bottom);
// Rotate the corners around the center of the rectangle
// AHA! Our units don't rotate around the center!
// Vector2 center = new Vector2(rect.Center.X, rect.Center.Y);
Vector2 center = new Vector2(rect.Center.X, rect.Top - (float)(UnscaledArrowheads * PieceSize));
for (int i = 0; i < corners.Length; i++)
{
corners[i] = RotatePoint(corners[i], center, angle);
}
return corners;
}
So, from the image, above, we know that these calculations are correct. Now, we need to flip the unit/sprite 180 degrees and we need to know the new location of the unit and rotation of the unit after the flip.
However, the unit isn’t flipping. These points are the same:
PointI PointA = BlueArmy[DisplayUnitIndex].Location;
PointI PointB = FlipUnit180Degrees(true, DisplayUnitIndex);
DistanceA = (int)UtilityMethods.EuclideanDistance(PointA, DestinationGoal);
DistanceB = (int)UtilityMethods.EuclideanDistance(PointB, DestinationGoal);
And here’s the (current) code for the flipping method (which is returning the same Point that it started off with):
public PointI FlipUnit180Degrees(bool side, int UnitID)
{
Vector2 point;
Point center;
Rectangle rec = new Rectangle();
Vector2 RPoint;
float tFacing;
if (side)
{
point = new Vector2((float) BlueArmy[UnitID].Location.X, (float)BlueArmy[UnitID].Location.Y);
rec = CalculateActualRect(BlueArmy[UnitID], BlueArmy[UnitID].Location);
center = new Point(rec.Center.X, rec.Center.Y - 6);
tFacing = (float)BlueArmy[UnitID].Facing;
}
else
{
point = new Vector2((float)RedArmy[UnitID].Location.X, (float)RedArmy[UnitID].Location.Y);
rec = CalculateActualRect(RedArmy[UnitID], RedArmy[UnitID].Location);
center = new Point(rec.Center.X, rec.Center.Y);
tFacing = (float)RedArmy[UnitID].Facing;
}
tFacing = (float)((tFacing + Math.PI) % (2 * Math.PI));
RPoint = RotatePoint(point,new Vector2(center.X, center.Y), tFacing);
PointI RPointI = new PointI(RPoint.X, RPoint.Y);
return RPointI;
}
Sorry for the long post. If anybody’s eyes can see something that I’m missing, it would be greatly appreciated.