What should be the preferred position type of objects in 2D games and how to handle collisions?

1

So I’m working on a game where the player controls a frog and shoots out its tongue and till now I handled all my position data with rectangles, mainly because of the “intersect” method already present, but the flaw in this methodology is that “int” is not very accurate as I’ve been getting some unpleasant results when drawing the tongue whilst the frog was rotating (Sometime the sections would not directly cover one another and would be drawn beside the previous section.

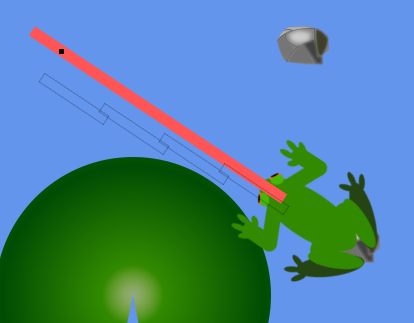
The red bar represents the tongue with Vector2, and the transparent represent the tongue with a rectangle, both use the same rotation variable and the rectangle gets its start position from the vector 2 location, but the results are the one seen above.

How do you guys handle “accurate” location and how do you then handle collisions?

2

There are XNA/MG Classes which have intersect functions like BoundingSphere, Ray, BoundingBox (that’s an AABB Box, so not practicable for your case).

You could go tru the hassle of implementing a transformed bounding box, but personally, I would represent your collision shape by a circle for the tip of the tong and two line-lists like so:

o=====[frog]

that’s fast, accurate and easy to implement - you maybe can get away with a single line-list for the tongues body, depending on your game.

a quick and dirty way without a lot of coding would be to just use a chain of circles … because circles are easy to collide (distance between them smaller then the sum of their radiuses)

1 Like
3

Do you think it would be best if I (just for collisions) adopt the BoundingSphere (tongue) and BoundingBox (enemy)?

4

The bounding box is axis aligned and I don’t think that will work good enough. If your enemies are circular, you can use a circle. The math behind circle collision is easy enough - not sure if you need the extra overhead of the 3D BoundingSphere.

Line intersection is a bit more complicated - the basic idea is to have a ray collision and use the distance of the intersection to see if it’s “on the line”

so, “best” is a bad word to use and highly depends on your math skills :slight_smile: I guess the easiest (but surely not the best) way is to use existing shapes like Ray or BoundingSphere. BoundingBox is AABB (Axis Aligned Bounding Box) - so as long as your enemies are not axis aligned, it may not work as you expect

5

Here is a line intersects method if you need it finding one or even the theory of one that isn’t bogus or written by someone who is dead wrong is like looking for a needle in a haystack.

        /// <summary>
        /// Very nice and works.
        /// from this dudes site  (i may have altered it a little but its based on this.)
        /// http://www.codeproject.com/Tips/862988/Find-the-Intersection-Point-of-Two-Line-Segments
        /// </summary>
        public static bool LineSegementsIntersect(Vector2 p1, Vector2 p2, Vector2 q1, Vector2 q2, out Vector2 intersection)
        {
            intersection = new Vector2();

            var r_pdif = p2 - p1;
            var s_qdiff = q2 - q1;
            var rxs = Cross(r_pdif, s_qdiff);
            var qpxr = Cross((q1 - p1), r_pdif);

            // If r x s = 0 and (q - p) x r = 0, then the two lines are collinear.
            if (rxs == 0 && qpxr == 0)
            {
                return false;
            }

            // 3. If r x s = 0 and (q - p) x r != 0, then the two lines are parallel and non-intersecting.
            if (rxs == 0 && !(qpxr == 0))
                return false;

            // t = (q - p) x s / (r x s)
            var t = Cross((q1 - p1), s_qdiff) / rxs;
            // u = (q - p) x r / (r x s)
            var u = Cross((q1 - p1), r_pdif) / rxs;

            // 4. If r x s != 0 and 0 <= t <= 1 and 0 <= u <= 1
            // the two line segments meet at the point p + t r = q + u s.
            if (!(rxs == 0) && (0 <= t && t <= 1) && (0 <= u && u <= 1))
            {
                // We can calculate the intersection point using either t or u.
                intersection = p1 + t * r_pdif;
                return true;
            }
            // 5. Otherwise, the two line segments are not parallel but do not intersect.
            return false;
        }

    public static float Cross(Vector2 v, Vector2 v2)
    {
        return v.X * v2.Y - v.Y * v2.X;
    }
3 Likes